キーワード:四元数、共役、絶対値
今回は、前回導入した四元数の計算がどのように行われるのかということを見ていきましょう。四元数の3つの虚数単位どうしの計算規則から、四元数の計算規則を導いていきたいと思います。また、複素数と同じように共役・絶対値が定義できることを確認します。また、四元数を用いた場合に方程式がどのようになるか、ということについても若干の注意をしておきたいと思います。
以下の議論では、
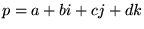 |
|
|
(1) |
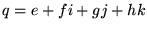 |
|
|
(2) |
とおく。
和と差については、各項ごとに計算すればいいので簡単です。
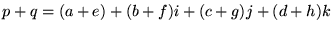 |
|
|
(3) |
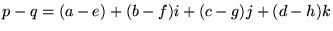 |
|
|
(4) |
これについて、特に注意点はないでしょう。
四元数の積については若干計算がめんどうです。これを簡単にするルールについては次回でやるとして、ここでは基本の計算規則を用いて計算してみましょう。
計算が長くなるので最後の項だけ計算してしまいましょう。
ここで 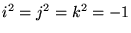 と
と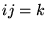 などを用いて変形しました。これを用いると
などを用いて変形しました。これを用いると
となります。これを見て、ベクトルの演算を知っている方はぴんとくるものがあるかもしれません。ですが、その話は次回のテーマとさせてもらいます。複素数と比べてもかなりややこしい計算になっていますが、これを整理する方法はありますので、今回はまず四則演算がきちんとできて閉じていることを確認してしまいましょう。また、別に計算した2行目の四元数になる部分については、積の順番を交換すると符号が変わります。四元単位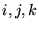 の積が交換しないことの影響で、一般に四元数の積は交換しません。
の積が交換しないことの影響で、一般に四元数の積は交換しません。
次に共役を定義しましょう。前回の因数分解の議論を踏まえれば、共役な四元数を
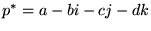 |
(10) |
と定義すれば
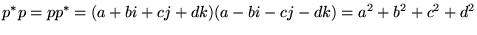 |
(11) |
となりますので、これを四元数の共役として問題なさそうです。上に書いたように、一般に四元数の積の順番は交換できませんが、それは結果に四元単位が現れるときだけです。結果が実数になる共役四元数との積は交換可能です。
またここに出てきた右辺の実数を、三平方の定理を踏まえれば四元数の「長さ」とみなしてよさそうです。これを絶対値といい、
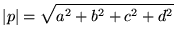 |
(12) |
で定義します。ここは複素数の自然な拡張として理解しやすいと思います。
以上の道具立てを用いて、商(割り算)を定義しましょう。
まずは、積の逆元を求めます。つまり、0でない四元数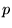 に対して、
に対して、
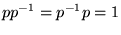 |
(13) |
となるような逆元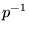 を求めてみましょう。といっても、前節の議論を用いれば複素数と同様に、
を求めてみましょう。といっても、前節の議論を用いれば複素数と同様に、
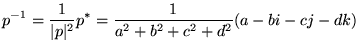 |
(14) |
と定義すれば、これが式(14)を満たすことはすぐ確認できるでしょう。
これを持ちいれば、
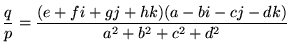 |
(15) |
となって、商が計算できます。
以上で、四元数に関しての和・差・積・商が定義でき、すべて四元数の中で閉じていることが確認できたと思います。
今回の話の最後に、四元数の困った性質について触れておきます。これは前回ちょっとだけ注意事項としてふれたことです。
いま四元数に関する方程式
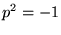 |
(16) |
を考えます。積の定義に当てはめると、
これを見れば、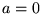 の「純虚」四元数ならば、絶対値1にすると自動的に
の「純虚」四元数ならば、絶対値1にすると自動的に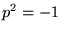 になることが分かります。つまり、
になることが分かります。つまり、
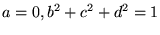 |
(19) |
を満たす四元数はすべて方程式(17)を満たします。
このように四元数では「代数学の基本定理」が成立しない。そういう意味ではすこしやっかいです。
今回は四元数の基本計算だったので少々退屈だったかもしれません。四元数において、複素数の拡張として四則演算を定義できることを確認したわけですが、とくに積のところは計算が複雑です。これが何を表しているのかなかなかイメージがつかみにくいかもしれません。次回は、この四元数の積に注目して、ベクトル演算との関係を用いて四元数の計算を見通し良く行う方法を見ていきたいと思います。また、それの応用として、逆にベクトルでは複雑になりがちな三重積を四元数を用いて計算してみたいと思います。
![]() に対して、
に対して、