| (1) |
| ホーム>物理・数学のページ>1.数学の基礎>1-11.四元数とベクトルの演算 |
前回は、四元数の計算規則を確認しました。今回は、特に積の計算をベクトルとの関係で見通し良くする方法について見ていきたいと思います。
前回も計算した純虚四元数の積を再掲します。
| (1) |
いま、二つの3次元ベクトルを ![]() とおきます。
とおきます。
ベクトルの内積 ![]() と外積
と外積 ![]() は、
は、
| (2) | |||
| (3) |
そこで、四元数 ![]() をスカラー
をスカラー![]() とベクトル
とベクトル ![]() を用いて、
を用いて、
| (4) |
| (5) | |||
| (6) |
| (7) | |||
| (8) |
前回、四元数の絶対値を導入したわけですが、一つ証明していないことがありました。それは積の絶対値がそれぞれの絶対値の積になるのかどうか、ということです。つまり、
たとえば、ベクトルのスカラー積、ベクトル積はそれぞれ、
| (10) |
| (11) |
の関係があります(ここで![]() は二つのベクトルのなす角)。積の絶対値がそれぞれの積とは異なるわけです。
は二つのベクトルのなす角)。積の絶対値がそれぞれの積とは異なるわけです。
いまここで、式(9)の両辺を2乗して、スカラー部、ベクトル部を用いて表してみますす。
一つ一つ計算していきましょう。
| (14) |
| (16) |
以上の結果を用いれば、
| (17) |
さて、前回の予告では3重積について書く、と言ったのですが、3重積自体の説明が難しくまだ整理できていないので、これについては保留というか、別の文章として線形代数のシリーズを作るときに反映させたいと思います。
その代りと言ってはなんですが、今回の最後に、四元数を「2重の複素数」として表すこと、そしてそこから量子力学で現れる「パウリ行列」との関係について示しておきたいと思います。
![]() において、四元虚数単位どうしの関係
において、四元虚数単位どうしの関係![]() を考慮すると、
を考慮すると、
| (18) |
つまり、複素数の中にもう一つ複素数が入っているような形になっています。そこで、第8回での議論を思いだし、![]() を行列にして、
を行列にして、
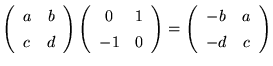 |
(20) |
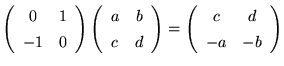 |
(21) |
これが反交換するためには![]() であればよいことがわかります。また2乗して単位行列の-1倍になるという性質も必要です。このような性質を持つ行列には任意性がありますが、もともと四元数を2重の複素数として表現した式を再現したいわけですから、それにもっとも近い形にするのが自然でしょう。そこで式(19)は、虚数単位を行列
であればよいことがわかります。また2乗して単位行列の-1倍になるという性質も必要です。このような性質を持つ行列には任意性がありますが、もともと四元数を2重の複素数として表現した式を再現したいわけですから、それにもっとも近い形にするのが自然でしょう。そこで式(19)は、虚数単位を行列![]() で書くならば、
で書くならば、
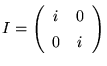 |
(22) |
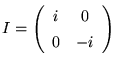 |
(23) |
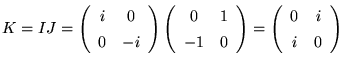 |
(24) |
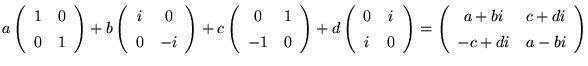 |
(25) |
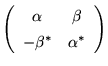 |
(26) |
ここで現れた3つの行列![]() は、物理学ではスピンの性質を表すために登場し、パウリ行列という名前がついています。複素数が2次元の回転を表していたのと同様に、四元数もなんらかの回転と関係していそうです。これは次回のテーマになります。
は、物理学ではスピンの性質を表すために登場し、パウリ行列という名前がついています。複素数が2次元の回転を表していたのと同様に、四元数もなんらかの回転と関係していそうです。これは次回のテーマになります。
現代の視点からは、今回みたように四元数は非可換の代数の一つとして理解され、またベクトルの演算との関連から整理されています。しかし、1843年にハミルトンが四元数を発見したときは、「交換則を捨てる」という大きな変革を記す第一歩として大きな意義があったと思います。
一方、ベクトルやその内積・外積の概念が出てくるのは四元数発見の翌年、1844年のことです。この年、グラスマンは「拡大論」を発表し、いまでいうところの線形空間論を構築しました。この中で一次独立などの概念ばかりでなく、内積・外積といった演算も導入しています。グラスマンは、数学上で線形代数や代数学の抽象化への道を作ったばかりでなく、外積を用いて正しく磁場と電流の間に働く力に関する式をたて、これが作用・反作用の関係を満たさないことを初めて示すなど、今に残る大きな仕事をたくさんしています(光の三原色の法則からサンスクリット語の研究までその業績は幅広い)。ですが発表当時、グラスマンの本は広く受け入れられたわけではなかったようです。そのせいか、いまでもグラスマンの名前はあまり有名とはいえません。私自身、場の量子論で「グラスマン数」というのを見るまで名前すら知りませんでした。最初にみたときは「グラスマンって誰?」と思ったぐらいです。後になって、数学・物理学の歴史、とくに電磁気学の歴史を調べる中でグラスマンの「偉大さ」に気付いたわけですが、もっと評価されてもいいのではないかと思います(残念ながら、日本語で読める資料は多いとは言えませんが)。
四元数の方は一時期大きく取り上げられ、マクスウェルが電磁気学の初期に用いたりしました。ハミルトンも、四元数を用いて物理学を書き換えるという壮大な事業に取り掛かりました。しかし、時代はハミルトン・グラスマンらのアイディアに触発されて大きく進み、結局テンソル解析(ベクトル・行列の微分・積分、微分幾何など)が発達して、その上に現代物理学が構築されていくことになります。
さて、次回はついにこの文章の最終テーマ「四元数と回転」についてです。一度は忘れられた四元数が、現代の3Dグラフィックスの世界によみがえることになったのは、四元数の演算が3次元における回転を効率よく表現できるからです。これは今回の前半のように1+3と分解して考えることによってその意味が明らかになります。次回ではまず最初に回転をどう表現するかという話からはじめ、次にそれを四元数を用いて記述するという形で展開していきたいと思います。