ホーム＞物理・数学のページ＞1.数学の基礎＞1-2.数を広げていく-有理数

第2回：数を広げていく‐有理数

キーワード：有理数、小数、稠密

割り算と逆数

前回、整数が和・差・積について閉じていることまでをみました。そして残っている計算は割り算です。

一般に、1は1以外の数字で割り切ることはできません。そこで、ある整数$ n$について、その整数と掛けると1になるような数を逆数とし、 $ \frac{1}{n}$と書くことにします。そして、一般の商$ n \div m$を

$\displaystyle n \div m = n \times \frac{1}{m} = \frac{n}{m} $

と分数で定義します。ここで$ n$と$ m$に公約数があった場合、 $ \frac{n}{m}$はほかの整数の商で表すことができます。

たとえば、 $ n=n' p , m=m' p$と書ける時($ p$は2以上の自然数)、これは約分でき、

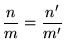
$\displaystyle \frac{n}{m} = \frac{n'}{m'} $

です。これ以上約分できないとき、その分数は既約であるといいます。

分数で表すことのできる数を有理数といいます。有理数の集合は $ \mathbb{Q}$と書きます。

有理数の計算についての説明は不要でしょう。

小数で表す

有理数の重要な性質として、小数で表すことができる、ということがあります。

当たり前のことと思うかもしれませんが、中学・高校の教科書で有理数と無理数を分けるポイントになっていますので、ちゃんと見ておきましょう。

たとえば、$ 1 \div 4$を小数であらわすことを考えます。

$\displaystyle 1 \div 4$ $\displaystyle = 0 \cdots 1$ (あまりの1を10倍する)    
$\displaystyle 10 \div 4$ $\displaystyle = 2 \cdots 2$ (あまりの2を10倍する)    
$\displaystyle 20 \div 4$ $\displaystyle = 5$ (割り切れた)    

以上のような計算の結果、 $ \frac{1}{4} = 0.25$となります。

割り切れない割り算の場合もあります。たとえば、

$\displaystyle 3 \div 7$ $\displaystyle = 0 \cdots 3$ (あまりの3を10倍する)    
$\displaystyle 30 \div 7$ $\displaystyle = 4 \cdots 2$ (あまりの2を10倍する)    
$\displaystyle 20 \div 7$ $\displaystyle = 2 \cdots 6$ (あまりの6を10倍する)    
$\displaystyle 60 \div 7$ $\displaystyle = 8 \cdots 4$ (あまりの4を10倍する)    
$\displaystyle 40 \div 7$ $\displaystyle = 5 \cdots 5$ (あまりの5を10倍する)    
$\displaystyle 50 \div 7$ $\displaystyle = 7 \cdots 1$ (あまりの1を10倍する)    
$\displaystyle 10 \div 7$ $\displaystyle = 1 \cdots 3$ (あまりの3はすでにでてきている)    

一般に、自然数$ n$で割ったあまりは$ n-1$以下の自然数であり、多くても$ n$回割り算を繰り返せば同じあまりが出てきます。よって、割り切れない場合でも有限個の数字を繰り返す循環小数であらわすことができます。今の場合、

$\displaystyle \frac{3}{7} = 0.\dot{4}2857\dot{1} $

と書きます。

よって、すべての有理数は有限回で割り切れるか、有限個の数字列が繰り返す循環小数のどちらかで表すことができます。

この表現には一つやっかいな性質があります。それは一意ではない、ということです。たとえば、

$\displaystyle x = 0.999999 \cdots = 0.\dot{9} $

を考えます。これは、

$\displaystyle 10x$ $\displaystyle = 9.99999 \cdots$ 両辺からxを引くことによって    
$\displaystyle 9x$ $\displaystyle =9$ よって    
$\displaystyle x$ $\displaystyle = 1$ $\displaystyle \qquad$    

よって $ 0.9999 \cdots = 1$です。これはいろいろな証明で問題になりますが、注意だけしておきます。

有理数の濃度

つぎに有理数の濃度を考えます。

ある無限集合を決まった順番にならべることができれば、それは自然数と同じ濃度、可算無限となるのでした。

有理数 $ \frac{n}{m}$には、$ m+n=l$が小さい順、そして$ m$が小さい順にならべます。そして、約分できるものを消します。

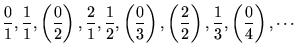
$\displaystyle \frac{0}{1},\frac{1}{1}, \left( \frac{0}{2} \right),\frac{2}{1},\... ...ght),\left( \frac{2}{2} \right),\frac{1}{3},\left( \frac{0}{4} \right), \cdots $

これで有理数に順番付けができました。よって

$\displaystyle n(\mathbb{Q}) = n(\mathbb{N}) $

です。

この順序付けはいわゆる大小関係とは違います。しかし、整数同様、有理数には大小関係＝順序を定義することができます。この点には深く立ち入りませんが、このような集合を順序集合といいます。

有理数は詰まっている

整数から拡張して有理数を作ったわけですが、これはどのくらい拡張されたのでしょうか。

数直線を考えたとき、有理数がそれをどのくらい埋め尽くすか考えます。

いま、適当な相異なる２つの有理数 x < y をとってきます。このとき$ x<z<y$となる有理数$ z$が必ず存在します。（たとえば $ \displaystyle{z=\frac{x+y}{2}}$をとることができます）

このように、ある（順序が定義された）集合の異なる2つの要素を取り出したとき、必ずその間にも要素があるとき、その集合は稠密である、といいます。ぎっしりつまっている、という意味です。

有理数の隙間

では、有理数はぎっしりつまっているということは、隙間はないのでしょうか？

そうではありません。有理数にはない数、というのを考えることができます。たとえば$ x^2=2$という数を考えますと、これは有理数ではありません。この証明は中学の教科書にも書いてあることなので割愛します。

同じような有理数でない数はいくらでも考えることはできます。それはこのような平方根（一般に累乗根）であらわされる数だけではありません。円周率$ \pi$や自然対数の底$ e$は、有理係数の方程式の解にはなっていません。

このように、有理数でない数をたくさん考えることはできます。では、どうやってこの有理数ではない数、をきっちりと考えることができるでしょうか。これが次回のテーマ、「実数の構成」です。