ホーム＞物理・数学のページ＞1.数学の基礎＞1-3.実数とは何か

第3回：実数とは何か

キーワード：実数・完備・連続

前回、有理数でない数、というのが存在するところで終わったのでした。

今回は、この有理数でない数、すなわち無理数というものが、どのようなものか考えていきたいと思います。

典型的な無理数としては、$ \sqrt{2}$のような平方根で表されるような数ですが、これ以外にも円周率$ \pi$や自然対数の底$ e$などがあり、この限りではありません。

どうやれば、有理数からつながりをもったまま、しかもその世界からはみ出すことができるでしょうか？

完備

いくつか言葉の定義をしておきます。

順序

集合$ X$の中で、関係$ \leqq$が定義されて、次の3条件が満たされるとき、順序という。

  1. 集合$ X$のすべての要素$ x$について$ x \leqq x$が成り立つ。（反射律）

  2. 集合$ X$の2つの要素$ x,y$について、$ x \leqq y$かつ$ y \leqq x$ならば$ x = y$（反対称律）

  3. 集合$ X$の3つの要素$ x,y,z$について、$ x \leqq z$かつ$ z \leqq y$ならば$ x \leqq y$（推移律）

もちろん普通の順序を念頭においておけばいいわけですが、対象とする集合によってはこの条件を満たす順序関係を定義しておく必要があります。いまは有理数を考えていますから普通の順序のことだと思ってください。順序が定義されると、次の有界集合を定義することができるようになります。

有界と上界・下界、上限・下限

集合$ A$が集合$ X$の部分集合であるとき、ある$ b \in X$があって、すべての$ a \in A$について$ a \leqq b$が成り立つとき、$ A$は($ X$の中で)上に有界であるといい、この$ b$を上界という。逆に$ b \leqq a$が成り立つならば、$ A$は下に有界であるといい、$ b$を下界という。上界に最小元があるならば、それを上限、下界に最大元があるならば、下限という。

この有界という概念が、有理数と実数を分ける重要な概念になります。

いま $ A = \{ 0 \leqq x, x^2 \leqq 2\}$という集合を考えます。これはすべての要素が、たとえば$ x \leqq 2$を満たしますから有界です。有理数のなかでは、この上界は最小元を持ちません。一方、これが実数の中でなら、上界は最小元$ \sqrt{2}$を持ち、これが集合$ A$の上限となります。

この違いを完備といいます。きちんと定義するならこうなります。

完備

集合$ A$のすべての部分集合が、上に有界ならば上限を持ち、下に有界ならば下限をもつとき、集合$ A$は完備あるいは順序完備であるという。

有理数から実数を作る前に先回りして定義してしまった感がありますが、これから実際に有理数を完備化して実数を構成してみます。しかし、実は完備化の方法は一つではありません。以下ではその一つであるコーシー完備化を説明しようと思いますが、切断による完備化などほかにも完備化の方法はありますし、厳密なことを言えば、コーシー完備は上の順序完備よりもゆるい条件であって同じではありません。しかし、有理数の完備化としてはどの方法をとっても同じものになることが証明されています。この辺のことは省略させてもらいます。

有理数列が有理数に収束するとは限らない

有理数から無理数へつなげていくためには、何か無限に関わる操作をしなければなりません。有限回の操作を行ったのでは、それはまた有理数になってしまうからです。

そこで、数に対する操作の繰り返しとして数列を考えます。その極限として無理数が出てくるようなものを考えるのです。

たとえば、

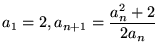$\displaystyle a_1 =2, a_{n+1} = \frac{a_n^2 + 2}{2a_n}$ (1)

という数列を考えます。いくつかこれを計算してみると、

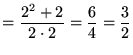$\displaystyle a_2$ $\displaystyle = \frac{2^2 + 2}{2 \cdot 2} = \frac{6}{4} = \frac{3}{2}$    
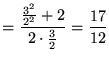$\displaystyle a_3$ $\displaystyle = \frac{\frac{3^2}{2^2} + 2}{2 \cdot \frac{3}{2}} = \frac{17}{4}$    
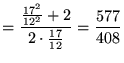$\displaystyle a_4$ $\displaystyle = \frac{\frac{17^2}{4^2} + 2}{2 \cdot \frac{17}{4}} = \frac{577}{408}$    

となります。これは、２から始まって加減乗除だけで計算していますから、どの項も有理数のままです。

さて、この数列は、どんどん差が縮まっていく性質を持っています。ε-δ論法で厳密に書くこともできますが、ここではそういう数列をコーシー列ということだけ覚えておきましょう。

この数列の一般項を書き下すことはできませんが、収束する値があるとすれば、その値$ \alpha$は $ a_{n+1}=a_n = \alpha$を満たすような数になります。この場合、

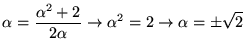$\displaystyle \alpha = \frac{\alpha^2 + 2}{2\alpha} \rightarrow \alpha^2 = 2 \rightarrow \alpha = \pm \sqrt{2}$ (2)

となって、初項2ではじめているので負にはなりませんから、その極限は$ \sqrt{2}$であることになります。

このように有理数の列があったとき、それがコーシー列になっていて極限をもっていたとしても、その極限がまた有理数の範囲に収まるとは限らないのです。これは前節の有界であるが上限をもたないのと同じことです。収束するということは有界なわけですが、その行き先がその集合自身に含まれているとは限らないわけです。

そこで、有理数のコーシー列の極限を有理数に付け加えれば、その集合はコーシー完備になります。これが実数です。（厳密にはもうちょっと違う方法をとります。コーシー列そのものに同値関係を導入し、それの商集合として実数を定義します。）

こうして、有理数から実数を作ることができました。一般にコーシー列がその集合の中で収束するように拡大することを「（コーシー）完備化」といいます。

実数の同値関係、加減乗除などもこの数列をつかって定義できますが、ここで厳密な議論を展開するつもりはないので割愛します。

さて、完備化の中でもコーシー完備化を取り上げたのは理由があります。それは最初の疑問、有理数と無理数だけですべて尽くされるのか、ということです。「数」を有限小数と無限小数に分けることができるということは、言い換えれば、すべての数は小数で表現可能ということです。これを保証するのがコーシー完備性です。次回はこのことと、実数の濃度について考えてみたいと思います。