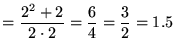 |
||
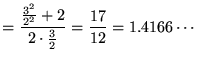 |
||
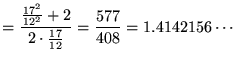 |
| ホーム>物理・数学のページ>1.数学の基礎>1-4.実数は数えられない |
さて、最初に目次のページで触れたように、実数は必ず小数で表すことができるのか、ということについて考えてみます。実数であるということは、その実数に収束する有理数のコーシー列が存在するということです。
ここで、前回の数列にもう一度登場してもらいましょう。ここで各項は有理数なので小数に展開できることが重要なポイントです。今回は分数を小数にしてみましょう。
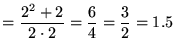 |
||
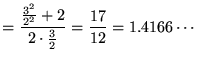 |
||
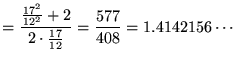 |
第4項でけっこう![]() に近くなってますね。もっと計算を続ければ、必要なだけ精度をあげて小数を計算することができます。つまり、実数はかならず小数で表すことができるのです。しかし、有理数の範囲ではけっして
に近くなってますね。もっと計算を続ければ、必要なだけ精度をあげて小数を計算することができます。つまり、実数はかならず小数で表すことができるのです。しかし、有理数の範囲ではけっして![]() そのものにはならないので、割り切れたり循環したりする小数ではありません。ここに無理数が無限小数になる理由があります。
そのものにはならないので、割り切れたり循環したりする小数ではありません。ここに無理数が無限小数になる理由があります。
やっと一つ目の疑問、実数とは何か、それは必ず小数で表されるものなのか、ということの答えに辿りつきました。もちろん、厳密な証明などをはしょっていますので、もっと本格的に勉強したい人はこの章の文末に参考文献を挙げておきましたのでそれで勉強していただきたいと思います。
次に、いままで自然数から有理数まで確認してきた「濃度」について考えたいと思います。
いままでの議論では、自然数も(その部分集合の偶数や奇数も)有理数も、可算無限という、大きさとしては同じ無限大の濃度を持つということを見てきました。さて、実数はどうなのでしょうか。
実数全体は0より大きく1未満の実数と1対1に対応させることができますので(適当な関数を与えることができます)、いま自然数と0より大きく1未満の実数とを比べることにします。
もし、この2つに1対1対応が作れたならば、これは「玉入れ方式」によって同じ濃度となります。なので、適当になにか対応表が作れたとしましょう。
さて、いまから、これが矛盾を含むことを示します。いま対応表の上から順に、1つ目から1桁目、2つ目から2桁目ととっていき、その数字を一つずらした(9なら0にする)数![]() をつくります。今の場合、
をつくります。今の場合、 ![]() です。これは、
です。これは、![]() 番目の数字とは、
番目の数字とは、![]() 桁目で必ず異なりますから、すべての表の数字と異なるものです。よって、1対1の表ではない、ということになります。この議論には、
桁目で必ず異なりますから、すべての表の数字と異なるものです。よって、1対1の表ではない、ということになります。この議論には、 ![]() のような一意性の問題がありますが、そういう表現はとりあえず禁止というか、同値ということにして、
のような一意性の問題がありますが、そういう表現はとりあえず禁止というか、同値ということにして、![]() に統一することにしておきましょう。こうした論法はよく用いられるもので、「対角線論法」と名前がついています。
に統一することにしておきましょう。こうした論法はよく用いられるもので、「対角線論法」と名前がついています。
こうして、自然数と実数の間には1対1の対応が作れないことが証明されました(厳密には選択公理などの前提が必要ですが)。自然数と対応できない実数がいくらでもつくれてしまうわけですから、実数のほうが多いということになります。
われわれは何気なく数直線というものを使ってきましたが、有理数まででは稠密(つまっている、2章参照)とはいえ、まだスカスカなのです。要素の個数としては実数のほうがずっと多く、実数まで考えてはじめて数直線を埋め尽くすのです。実数のこの性質を連続性といいます。
実数の個数は不可算無限と呼ばれ、可算無限とはレベルのちがった無限大ということになります。
では、自然数の個数、すなわち可算無限と比べてどのくらい多いのでしょうか。
ここで厳密な議論を展開する力は私にはありませんが、イメージとしては次のように考えることができます。
すべての実数は小数に展開することができます。そのとき数字は10進数である必要はなく、最小では2進数ということになります。実数を2進小数で表したとき、0か1の列が可算無限個続くわけですから、この場合の数は便宜的に、可算無限個を![]() 、不可算無限を
、不可算無限を![]() と書けば
と書けば
| (1) |
ところで、可算無限と不可算無限という2種類の無限大があることが分かったのですが、ほかに無限大はないのでしょうか。いまのところ、可算無限がもっともちいさい無限大であることは分かっています。実は大きな無限大というのはいくらでも作れます。上の関係のように、べき集合を考えていくことで、いくらでも濃度が本質的にことなる、より大きな無限大を考えることができます。
しかし、未解決の問題もあります。可算無限と不可算無限の間の大きさをもつ無限大は存在するか、という問題です。そういうものはない、とするのが「連続体仮説」です。つまり、可算無限の次の無限大が実数(連続体)の濃度だということです。これはあくまで仮説というか、公理のようなもので、ほかの実数の性質や集合論の公理などから証明も否定もできない、独立したものだということが分かっています。不完全性定理で有名なゲーデルが否定的、つまり中間の無限大もあるだろうという立場だったそうですが、実際にそういうものが発見されているわけでもなく、いまのところどっちが正しいと決定できる状況ではありません。これについては現在の集合論の公理系(ツェルメロ・フレンケルの公理系+選択公理)に何か足りないのではないかという議論がなされているようですが、これ以上つっこんだことはいえません。
ここまでの議論をまとめましょう。数を広げていく、ということで、自然数に始まり、整数、有理数、そして実数へと広がっていく様子をみてきました。そして、濃度(集合の要素数)という面で、実数だけは別格だということ、それが「連続」であることにつながっていることを見ました。
ここでの議論は数学基礎論といわれるように、数学のもっとも基礎の部分を形作っているものです。ここからさらに議論を深めていくこともできます。
このような小さな集合から拡大してより大きな概念へと広げていくやり方、いわばボトムアップの議論とは逆に、最初に連続な集合(つまりは実数)というものがどのような性質を満たすべきかという公理群を与え、そこから議論を展開していく、いわばトップダウン的な議論もあります。どちらかというと、解析学としては後者のほうが議論を展開しやすいですし、その中で連続のもつさまざまな性質の議論がされますから、そのような公理論的な実数論も重要なのですが、そういったことについては解析学についての基本的な教科書を参照していただきたいと思います。
また、今回のように、最小の性質をもった集合にどのような性質を加えていけば必要な集合になるのか、という議論の進め方は、このあと、位相空間、距離空間といった議論があるのですが、これはそのうち、微分幾何学や物理学とホモロジー・ホモトピーといったことについて書くことがあれば触れることになるでしょう。
今回の連載としては、これからも数の拡張という方向性を続け、次回からは代数的な方向に進んでいきたいと思います。そして複素数・四元数へと数が広がっていく様子についてみていきます。
|
|
自然数から始まって実数を構成していくタイプの議論をきちんと勉強したいのならお勧めの本。今回の話ではコーシー完備化だけ扱って順序完備化をきちんと説明してなかったり、いくつかはしょったところを埋めたい方はどうぞ。また付録で公理論的集合論の基礎も扱っている。そういえば、この連載のタイトルと同じタイトルだ・・・これからの議論の方向性はぜんぜん違いますが。
|
| 公理論的に実数を組み立て、そこから連続性とは何か、そしてさらに微分・積分を組み立てていく本。大学初年度の微分積分の本より一歩深いところから説き起こす。とくに積分に関する詳しい議論を勉強したい場合とても参考になる。2巻目も含めるとベクトル解析や複素解析の基本も勉強できる。
ただ、最初に微分積分を学ぶなら、もっと計算主体の本がいいと思います。というか、自分ももともと物理屋なもので、こういう議論は正直苦手でした。何度も読み返し、演習などを解くことで解析の基礎が身についていく感じです。微分方程式や計算のほうを勉強したい場合は別の本から入ったほうがいいかもしれません。 前書きをみると、教養1年の解析の授業で使うと書いてある。1年生でこれやるとは、東大おそるべし。まあ(出版された)1980年ごろの話で今は違うのかもしれない(いまでは高校数学の教育課程がぜんぜん違うので)。 |