| (1) |
| ホーム>物理・数学のページ>1.数学の基礎>1-5.代数方程式と複素数 |
これまでは自然数に始まり、整数、有理数、実数と数を広げてきました。そこには引き算、割り算、平方根などの、新しい問題(計算)を、数の概念を広げることによって解けるようにしていくという流れがありました。今回からは、もっと一般の「代数方程式」というものを考え、それを解くためには何が必要なのかを見ていきます。
今回からは代数の話に入っていきます。まずは多項式を定義しておきます。
と書き表される式を(n次)多項式と言います。そして![]() の形にかける方程式を代数方程式と呼びます。
の形にかける方程式を代数方程式と呼びます。
おなじみなのは、1次方程式や2次方程式でしょう。
これまでの議論も、「方程式の解」という観点でまとめることができます。
たとえば、負の数![]() は、1次方程式
は、1次方程式
| (2) |
| (3) |
平方根は、もっとも簡単な2次方程式
| (4) |
実は、実数というのは代数方程式の範疇だけで考えられるものではありません。たとえば円周率![]() を、有理数だけを用いた代数方程式の解として求めることはできません(こういう数を超越数といいます)が、今回は代数方程式の方向で話を進めていきたいと思います。
を、有理数だけを用いた代数方程式の解として求めることはできません(こういう数を超越数といいます)が、今回は代数方程式の方向で話を進めていきたいと思います。
一般の2次方程式、
| (5) |
とくに「解の公式」、
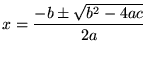 |
(6) |
と持ち上げたところで、これに待ったをかけるような方程式が現れます。
| (7) |
まずは、めんどくさいルートの中から計算しておくといいですね。やってみましょう。 ![]() を公式に代入します。
を公式に代入します。
| (8) |
私が中学生だった1○年前はこういう問題も出まして、「解なし」と習ったものです。最近の中学の教科書やら入試問題集では、こういう方程式の存在は無視され、ないことにされているようです。(2012年度からまた指導要領が変わりますので、この辺の事情は変化するかもしれません)
ちょっと上では「最終兵器」とか言っておきながら、難攻不落、絶対に解けない2次方程式があるのです。それはそもそも「解がない」のだから解きようがないということになります。
2次方程式の解の公式の原型は、古くバニロニアの時代からあったようですが(もちろん当時はまだ負の数の概念もありませんから、今のような形にはなりませんが)、少なくとも5世紀から6世紀にかけてのインドでは今のような形で存在したようです(フワリズミの代数学)。しかし、そこでは当然「負数の平方根(![]() など)」というのはあり得ない数として避けられてきました。
など)」というのはあり得ない数として避けられてきました。
その状況が変わるのは3次・4次の代数方程式の解の公式が発見される16世紀ごろになってからです。この解の公式を計算する過程で、最終的な解が実数解になる場合でも、計算途中に負数の平方根を(形式的にであっても)使わなければならないという状況が発生したのです。
当初、これはあくまで便宜的なものであって、実際はありえない数とされてきました。これを覆し、負数の平方根も認めようとしたのはガウスです。
ガウスは、次に述べる「代数学の基本定理」を証明する際に、負数の平方根を認めれば、すべての代数方程式に解が存在することを証明しました。いまでは、負数の平方根を虚数(imaginary
number)と呼び、特に-1の平方根を記号![]() で書くことが多いです(つまり
で書くことが多いです(つまり ![]() )。「imaginary=想像上の」、あるいは「虚」という語にあるように、当時は実在の対応物を持たない、概念上のものとされたようです。しかし、ガウスはすぐに複素平面のアイディアを具体化し、複素数(
)。「imaginary=想像上の」、あるいは「虚」という語にあるように、当時は実在の対応物を持たない、概念上のものとされたようです。しかし、ガウスはすぐに複素平面のアイディアを具体化し、複素数(![]() の形に書ける数)が平面上の点と対応することを示しました。複素平面についてはこの文章の別の章を割り当てて詳しくみることにしたいですが、現代の物理学では、波動関数、あるいは状態と呼ばれる基本的な量が本質的に複素数であり、虚数なしには物理を表現することは難しくなっています。その意味では、もう「虚」という言い方は実態を表していないといえるかもしれません。
の形に書ける数)が平面上の点と対応することを示しました。複素平面についてはこの文章の別の章を割り当てて詳しくみることにしたいですが、現代の物理学では、波動関数、あるいは状態と呼ばれる基本的な量が本質的に複素数であり、虚数なしには物理を表現することは難しくなっています。その意味では、もう「虚」という言い方は実態を表していないといえるかもしれません。
ここでは、虚数・複素数の性質と基本的な計算について確認しておきましょう。
もう一度、定義からはじめます。虚数単位![]() を、
を、
| (9) |
| (10) |
普通の実数(real number)と純虚数の和になる数を複素数(complex number)といいます。
| (11) |
形としては ![]() と似た形をしていますが、普通の平方根を使った数は数直線上にありますが、この複素数はもはや数直線だけで表すことはできません。その辺の事情はまた場所を改めて解説していきたいと思います。ここでは、複素数の上に加減乗除の計算を定義しましょう。和と差については、平方根の計算と同じようにできます。二つの複素数
と似た形をしていますが、普通の平方根を使った数は数直線上にありますが、この複素数はもはや数直線だけで表すことはできません。その辺の事情はまた場所を改めて解説していきたいと思います。ここでは、複素数の上に加減乗除の計算を定義しましょう。和と差については、平方根の計算と同じようにできます。二つの複素数 ![]() があったとき、この2数の和と差は、
があったとき、この2数の和と差は、
| (12) |
| (13) | ||
| (14) | ||
| (15) |
次は商ですが、その前に複素数の逆数について計算しておきましょう。これは「分母の有理化」の要領です。
| (16) | ||
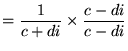 |
(17) | |
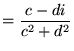 |
(18) |
これらを用いれば、複素数の商は次のようになります。
| (19) | ||
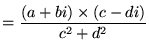 |
(20) | |
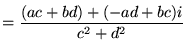 |
(21) |
積と商については、形も複雑ですし、慣れないうちは大変かと思います。積と商の意味するところについては、第7章の複素平面で考えるとより明確になるかと思います。
ひとつ変わった点は、複素数はもはや順序体ではないということです。なので順序完備ではありません。しかし、連続性などの性質はもっていますから、ほとんどの議論は十分成立します。
とりあえず、負数の平方根を認めて複素数を作ったときに、矛盾なく加減乗除という計算が定義でき、自然に数を拡張することができるということを確認してください。
では、3次方程式以降はどうなのでしょうか?3次方程式の解を表現するには、また新しい虚数のようなものを導入して数を広げる必要があるのでしょうか?
その答えは「No」です。逆に言えば、複素数を認めてしまうと、すべての代数方程式に解が存在することが証明できます。これを「代数学の基本定理」といいます。この代数学の基本定理を証明することは、代数学の力だけではできません。複素関数論という解析学(微分・積分)の定理か位相幾何学の定理を使わなければならないのです。こういうところも数学の面白いところです。一応、幾何学・代数学・解析学などと分野が分けられていますが、それぞれが独立であるわけではなく、お互い別の分野の成果を用いて成立している部分があり、やはり数学は全体で一つの学問分野として成り立っているわけです。
さて、今回のメインディッシュ、代数学の基本定理の証明に行きましょう。ですが、厳密に展開せず、ストーリーというか大まかな流れだけを見たいと思います。ここでは、一般的に目に触れる解析的な証明を紹介します。(そのうち、どこまで代数的な知識だけで証明できるのか、といったマニアックなテーマも追及してみたいですが)
命題は、「多項式(1)について、![]() を満たす複素数
を満たす複素数![]() が少なくとも1つ存在する」ということである。証明は大きく分けて2段階あります。
が少なくとも1つ存在する」ということである。証明は大きく分けて2段階あります。
第1段階。まず実数値関数としての![]() は、複素数上で最小値を持つ。
は、複素数上で最小値を持つ。
第2段階。実は、その最小値は0である。
以上より、![]() になるのは、
になるのは、![]() になるときに限るから、結局、
になるときに限るから、結局、![]() となる点が存在することになる。
となる点が存在することになる。
まずは第1段階を示そう。
![]() をどんどん絶対値の大きな値に変えて行ったとしよう。このとき、
をどんどん絶対値の大きな値に変えて行ったとしよう。このとき、![]() もどんどん大きくなる。ちゃんと書けば次のようになる。
もどんどん大きくなる。ちゃんと書けば次のようになる。
この最小値![]() は、
は、 ![]() なので、
なので、![]() では
では ![]() となって、結局複素数全体の範囲にわたっての最小値になる。これで第1段階が終了です。
となって、結局複素数全体の範囲にわたっての最小値になる。これで第1段階が終了です。
第2段階。言い換えて、 ![]() ならば、かならず
ならば、かならず ![]() となる複素数
となる複素数![]() が存在することを示します。
が存在することを示します。
これについては、計算の技巧的になってしまうので詳細は省きますが、適当な方向へちょっとずらしてやれば、![]() でない限り、絶対値をさらに小さくすることができます。厳密な証明については解析あるいは線形代数の教科書などを参照してください。
でない限り、絶対値をさらに小さくすることができます。厳密な証明については解析あるいは線形代数の教科書などを参照してください。
これにより、結局、第1段階の最小値![]() は0でなければならないことになります。
は0でなければならないことになります。
第1段階で使っている連続性、第2段階で使っている性質、それぞれが代数的というより解析的な性質なわけですね。
「代数学の基本定理」については、ダランベールやラプラス、オイラーといった数学者たちが挑戦し、ガウス単独のものではありませんし、どうやらガウスの証明も厳密には穴があって先取権は別の数学者かもしれないという説もあります。数学史にもまだまだ取り組むべきことは多いようです。
数を広げるという観点から、今回は複素数を導入しました。これによって、すべての代数的な方程式に解の存在が保障されます。
最終目標の四元数まではもう一息なのですが、その話に入る前にもう少し方程式について話をしておきたいと思います。方程式に解が存在することは分かったとして、その解を見つけることができるか、という問題が残っているからです。2次方程式には解の公式が存在しました。それ以上の方程式にも解の公式があるのかというと、5次以上では存在しないことが証明されていることは上にも書きました。それでは解を求めるにはどうしたらいいのでしょうか?次回は、因数定理とそれを応用した方程式の解法について触れたいと思います。
そして、その次からは複素数のさまざまな側面を検討する中で、四元数へと近づいていきたいと思います。