ホーム＞物理・数学のページ＞1.数学の基礎＞1-6.因数定理と代数方程式の解の探し方

第6回：因数定理と代数方程式の解の探し方

キーワード：剰余定理・因数定理・代数方程式の解法

代数方程式の代数的解の公式

すべての代数方程式に解が存在することがわかりました。では、その解を実際に求めるにはどうしたらいいでしょうか？

2次・3次・4次の方程式には解の公式があることはすでにふれました。つまり、4次以下の方程式には必ず解を求める方法があるのです。

しかし、5次以上の方程式には代数的な解の公式は存在しません。見つかっていないのではなく、「作れないこと」が証明されているのです。「代数的」というのは加減乗除や累乗根を使って、という意味です。

これはアーベルやガロアの理論によるもので、抽象代数学・群論という分野の話になってきます。これを話すにはまた別の道具立てが必要ですから、機会があればどこかで触れたいと思います（群論についてはこの文章の流れのなかで触れるつもりではいます）。

とにかく、5次以上になると解があるのにそれを絶対に見つける方法はないということになってしまいます。やはり、必ず解くことができるという安心感を与えてくれるという意味で、解の公式があるということは素晴らしいことではないでしょうか。

もちろん、どうにかして解くことができる場合もあります。その糸口を見つけてくれるのが次に説明する「因数定理」です。

実は「代数的」でないならば解の公式は存在します。それは楕円関数などの「解析的」道具を借りてくることによって作れるのですが、解析学の話はしていませんし、実用的にも計算量が多すぎて使えないのでこれについては省略させてもらいます。

次節では、2次方程式を解くときにも大変お世話になる「因数分解」を使った解法について話していきましょう。

因数分解と方程式：剰余定理と因数定理

2次方程式を解くときも、それが「因数分解」できるときは解の公式を使うまでもなく解けます。この話を一般化しましょう。

多項式$P(x),Q(x)$について、割り算$P \div Q$というのを考えてみます。もちろん$P(x)$の次数が、$Q(x)$のそれと同じか大きくなければ割れません。いま、

$$P(x) = Q(x) \cdot D(x) + R(x)$$

と書けるとき、$D(x)$を商、$R(x)$を剰余といいます。これは普通の割り算と同じ感覚で理解していただければいいでしょう。

このとき、それぞれの多項式の次数を$p,q,d,r$で表すなら、$p=qd$かつ$q>r$です。とくに、$Q(x)$が1次式 $ax+b(a \neq 0)$ならば、剰余項$R(x)$は定数になります。すなわち、

$$P(x) = (ax+b) \cdot D(x) + R$$

です。よって、$x = -b/a$を代入すれば $P(-b/a) = R$となります。これを剰余定理といいます。

そして、ちょうど$P(x)$が$(ax+b)$で割り切れるとき、つまり$R=0$のとき、$P(-b/a)=0$となって、$x = -b/a$は$P(x)=0$の解になります。これを因数定理と呼びます。

こうして、代数方程式を解くことと、多項式を因数分解することは同じことになります。これを利用すれば、高次の多項式を解くこともできるわけです。

たとえば、 $x^3+2x^2-x-2=0$という方程式を考えてみます。

ぱっとみてわかるのは、$x=1$を代入すると$1+2-1-2=0$となり、これが解になっていることです。

そこで、これは$(x-1)$で因数分解できるはずで、

$$x^3+2x^2-x-2=(x-1)(x^2+3x+2) = (x-1)(x+1)(x+2)$$

と因数分解できますから、結局解は $x=\pm 1,-2$の３つであると求まります。

このように一つの解を見つけることで、それを使って因数分解していけば次々に次数を減らすことができ、方程式を解くことができる場合があります。

もう一つ例をあげましょう。

数学検定1級(第161回)に過去出題された問題で、 $x^4-4x-1=0$を解け、というものです。

前の問題とちがい、ぱっとみてすぐに代入して分かる解はありません。では、どうしたらいいでしょうか。

これは因数分解をどうにかしてやってみるというしかありません。

ちょっと技巧的になりますが、

$$x^4-4x-1 =(x^4+2x^2+1)-(2x^2+4x+2)=(x^4+2x^2+1)-2(x^2+2x+1)$$

$$=(x^2+1)^2-(\sqrt{2}(x+1))^2$$

$$=(x^2+\sqrt{2}x+(1+\sqrt{2}))(x^2-\sqrt{2}x+(1-\sqrt{2}))$$

それぞれを解の公式をつかって解けば、

$$x = \frac{-\sqrt{2} \pm \sqrt{4\sqrt{2}+2}i}{2}$$

$$x = \frac{\sqrt{2} \pm \sqrt{4\sqrt{2}-2}}{2}$$

となります。

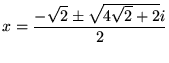
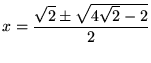
このように因数分解すれば解ける場合もあります。

2次方程式に分解する

実はこの問題をもう少し「力技」で解くこともできます。

その前に一つ、武器を作りましょう。

「共役複素数」というものを考えます。これは$z=a+bi$に対して $\bar{z}=a-bi$と虚数部の符号を変えたものを「共役」と呼びます。これについてのいくつかの性質を書いておきましょう。

$$z + \bar{z} = 2a$$

$$z - \bar{z} = 2bi$$

$$z \times \bar{z} = a^2 + b^2 = \vert z\vert^2$$

$$\overline{\mathstrut{\alpha}} \times \overline{\mathstrut{\beta}} = \overline{\alpha \times \beta}$$

とくに、

$$\overline{z}^n = \overline{z^n}$$

とりあえず、ある複素数と共役複素数の和・積は実数になることを覚えておきましょう。また、実数の共役はその実数自身です。

さて、ここで実数係数の方程式$f(z)=0$が複素解$z=\alpha$を持つとしましょう。そうすると、$f(z)$の係数はすべて実数ですから、 $f(\bar{z})=\overline{f(z)}$です（具体的な多項式で確かめてみればわかると思います）。なので、この解と共役な複素数も、 $f(\bar{\alpha})=\overline{f(\alpha)}=0$となって、元の方程式の解になります。つまり実数係数の方程式が複素数の解をもつならば、それと共役な複素数も解である、ということが言えます。

そこで因数定理によって、この方程式は $(x-\alpha)(x-\bar{\alpha})$で割り切れるはずです。ところで、この式は、

$$(x-\alpha)(x-\bar{\alpha}) = x^2-(\alpha+\bar{\alpha})x+\alpha\bar{\alpha}$$

と展開できますが、$x$の係数も定数項も、どちらも先に書いたように実数ですから、この2次式は実数係数になります。

よって、実数係数の多項式は、かならず実数係数の1次式あるいは2次式で因数分解することができるということがいえます。

さて、これを踏まえて先の4次方程式の問題にアタックしてみましょう。これが2次式で因数分解できるのですから、

$$x^4-4x-1=(x^2 + ax + b)(x^2+cx+d)$$

と無理やりおいてみましょう。すると展開して係数を比べることで、

$$a + c = 0$$ (1)

$$b + d + ac = 0$$ (2)

$$ad + bc = -4$$ (3)

$$bd = -1$$ (4)

ということが分かります。4つの未知数に4つの方程式ですからこれは解けそうです。結局もとの4次方程式に戻ってしまったりしたら意味がないですが、これは解くことができます。普通に$c=-a$と$d=-1/b$とおくことによって文字を減らし、残りの二つを使えば面倒な計算にはなりますが、難しくはないと思います。

結果、前と同じ因数分解の結果を得ることができます。前の解法では項を足し引きして少し技巧的に解いていましたが、それを思いつかなくても無理やり2次式に分解して解くこともできるわけです。

コンピュータを使えば、与えられた多項式に対してそれを因数分解できる2次式を探し出すこともできます。これはベア・ストウ法とよばれる計算方法として知られています。機会があれば実際のプログラミング例をアップしたいと思います。

まとめ

今回は実際に方程式を解く、ということに焦点を当てましたが、もう一つの目的は因数分解と因数定理について書いておきたかったというのがあります。たとえば、$x^2+1$は実数の範囲ではこれ以上因数分解できませんが、複素数を使うことを認めれば $(x-i)(x+i)$と因数分解できてしまいます。これの延長上に、最終目標である四元数があるのです。

ですが、ここではまだ四元数の話にいく前に、複素数についてもう少し掘り下げておきたいと思います。次回は、複素数の幾何学的な性質、「複素平面」についてみていきます。これによって、複素数の積と商についての「イメージ」がつかめると思いますし、平面幾何学と複素数の関係も見えてきます。そして、これがのちに四元数を幾何学的に理解する助けになるはずです。