| (1) | |||
| (2) | |||
| (3) |
| ホーム>物理・数学のページ>1.数学の基礎>1-8.数学をルールから捉える―抽象代数学・群について |
今回の話は、少しわき道にそれるようにも見えるかもしれません。しかし、四元数の性質を考える前に、計算のルールに着目した考え方である「抽象代数学」について触れておきたいと思います。というのも、四元数はこれまでの複素数と違ったルールで計算されるからです。そういうものにいきなり触れるよりも、もっと分かりやすい例を交えて、計算ルールの自由度について考えておくのはよい準備になると思います。
私たちは、ふだん何気なく次のような計算をしています。
式(1)や(2)のような計算が可能であることを「交換則」といいます。これは計算の順番を交換しても結果が変わらないことをいいます。和や積とは違い、差や商は計算の順番を変えてしまうと結果が変わってしまいます。こういう計算は「交換則が成り立たない」といいます。
一方、式(3)の計算は、「分配則」といいます。かっこを外す計算をするときの基本ルールです。これは和を差に変えても成り立ちますが、積を商にした場合は、右からの割り算のとき、すなわち ![]() の場合のみ成り立ちます。
の場合のみ成り立ちます。
さて、この話を一般化しましょう。
まず集合Sを考えて、そのうえでの演算「![]() 」を考え、これがS上で閉じているとします。つまり、Sの元
」を考え、これがS上で閉じているとします。つまり、Sの元![]() があったときに、
があったときに、![]() もまたSの元になっているとします。
もまたSの元になっているとします。
このとき、以下の条件をすべて満たすならば、集合Sは演算![]() について、群をなす、といいます。
について、群をなす、といいます。
これは、普通の実数や複素数が和や積(積の場合0を除く)について成り立っていることはすぐにわかると思います。
さらに
ここで交換則を別格に扱ったことには意味があります。今まで出てきたような普通の数は、交換則も成り立つ加群を構成していました。しかし、数学で扱う対象を広く考えるならば、むしろこのような性質をもつものは少なく特殊な例といえます。そこで、より広い「群」を考え、それへのさらなる付加条件として交換則をもつ群として加群を定義しています。
数学の対象となるもので、加群ではない例としてまず挙げられるのが、行列でしょう。
行列は、たとえば以下のような2行2列の正方行列があります。
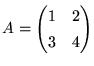 |
(4) |
行列の積は、たとえば2次の正方行列![]() の積ならば以下のように定義されます。
の積ならば以下のように定義されます。
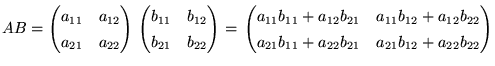 |
(5) |
この積は群を作りますが、一般に ![]() となることは容易に確かめることができると思います。
となることは容易に確かめることができると思います。
また、ベクトルの外積と呼ばれる計算も、交換則を満たしません。これは、一般に
| (6) |
行列やベクトルの積についての詳細は線形代数学の教科書を参照してください。
先取り的にいうと、複素数は実数になるときに順序体であることを捨てました。四元数はさらに可換性を捨てるのです。そうやって計算のルールの制限を取り除くことによって、より複雑な構造を獲得するといってもいいでしょう。このような拡張は、次に結合則を捨てる八元数で群を作るものは終わりになりますが、そこまでの話をするつもりはありません。こういった議論を紹介しているのは、多分に最終的な目標である量子力学(場の量子論)を意識して作っています。光などの相互作用はボソンと呼ばれ、交換する世界に属します。いっぽうの電子などの物質はフェルミオンと呼ばれ、反交換の世界に属しています。そこでは、計算ルール(代数)が大きな役割を果たしているのですが、そういう話もいずれはどこかで書きたいと思っています。
数以外でも群を作ります。たとえば、次のような3文字の文字列を考えます。
| (7) |
| (8) |
また、図形の変形なども群を作ります。たとえば、図形を平行移動・回転・鏡映変換(左右逆にする、線対称ともいう)したとき、図形の形と大きさは変わりません。そしてこれらの変形を繰り返し行っても形と大きさが変わらないという性質は保たれたままです。これらの変形を合同変換といい、これも変換の合成を積とみなせば群を作ります。
ここで、正6角形を不変に保つ変換について考えてみましょう。これは頂点を別の頂点に移す変換として考えることができ、60度の整数倍の回転と、3本の対角線および対辺の中点を結んだ3本の線を軸とした鏡映の合計12種類が考えられます。いまはこのうち6個の回転を考え、これを ![]() としましょう。
としましょう。
![]() は0度(360度)の回転で、これが単位元(元に戻る変換)
は0度(360度)の回転で、これが単位元(元に戻る変換)![]() になっています。また二つの回転を合成したものは、角度を足したものになっていますから、これも6個の回転のうちのどれかに(360度の差を無視すれば)同じになります。また60度に対して300度の回転といった逆元が存在します。さらに交換則も成り立つことも確かめられます。以上のことから、この変換は一つの加群を構成することが分かります。
になっています。また二つの回転を合成したものは、角度を足したものになっていますから、これも6個の回転のうちのどれかに(360度の差を無視すれば)同じになります。また60度に対して300度の回転といった逆元が存在します。さらに交換則も成り立つことも確かめられます。以上のことから、この変換は一つの加群を構成することが分かります。
さて、恒等写像を![]() 、60度の回転を
、60度の回転を![]() とすると、
とすると、 ![]() となり、
となり、![]() と6個目でもとに戻ります。このように積を繰り返していくと恒等写像に戻るような群を「巡回群」といいます。
と6個目でもとに戻ります。このように積を繰り返していくと恒等写像に戻るような群を「巡回群」といいます。
この「6乗すると単位元になる」という性質はこの回転による群だけではありません。複素数の世界で考えて、
| (9) |
| (10) |
さらにいえば、60度の回転を表す行列
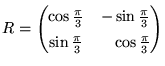 |
(11) |
次節では行列の作る群について、もう少し分類をしておきたいと思います。これは少し専門的になりますが、表現の話だけでなく、四元数や場の理論といったさまざまなものと関連する事柄なのでいまのうちに触れたいと思います。(というか、この話をするためにこの章を設けているといってもいいかもしれません)
まず一番広い群は正方行列の作る群で、![]() 次の一般線形群(general linear group)
次の一般線形群(general linear group)![]() あるいは実数を要素にするという意味で
あるいは実数を要素にするという意味で ![]() と書きます。複素一般線形群ならば
と書きます。複素一般線形群ならば ![]() です。
です。
これに条件をつけたもので群を構成するものがあります。これらは群の部分集合が群になっていると意味で部分群と呼ばれます。
まず大きなくくりとして行列式が1になるものに限定します。行列式は行列の積に対して ![]() が成り立ちますから、行列式が1になる行列同士をかけるとその結果も行列式が1になります。よって、これは群を作り、特殊線形群
が成り立ちますから、行列式が1になる行列同士をかけるとその結果も行列式が1になります。よって、これは群を作り、特殊線形群 ![]() (複素係数なら
(複素係数なら ![]() )と呼ばれます。以下、「特殊」=「行列式=1」と読み替えてください。また一般的に、複素数は1つの要素について実部・虚部の2つの変数があることとになりますので、その自由度(独立な変数の数)は倍になります。
)と呼ばれます。以下、「特殊」=「行列式=1」と読み替えてください。また一般的に、複素数は1つの要素について実部・虚部の2つの変数があることとになりますので、その自由度(独立な変数の数)は倍になります。
次に実行列のうちで、
| (12) |
この直交群に「行列式=1」の条件をさらに加えたものが特殊直交群![]() で、これは先ほど出てきた回転行列のことですから、回転群とも呼ばれます。直交行列の定義から、
で、これは先ほど出てきた回転行列のことですから、回転群とも呼ばれます。直交行列の定義から、 ![]() (
(![]() は単位行列)であることを用いて、転置行列の行列式が元の行列と同じことに注意すると、
は単位行列)であることを用いて、転置行列の行列式が元の行列と同じことに注意すると、
| (13) |
次に複素行列の例を考えましょう。![]() の複素共役行列
の複素共役行列 ![]() (右上の記号は「ダガー」と読みます)を
(右上の記号は「ダガー」と読みます)を ![]() つまり転置してすべての要素を複素共役したものとして定義します。このとき、
つまり転置してすべての要素を複素共役したものとして定義します。このとき、
| (14) |
これらのほかにも実行列では交代行列(転置が元の行列の-1倍になる)や、複素行列のエルミット行列など、群を作るものはたくさんありますが、このくらいにしておきます。
前節の議論を踏まえると、上に出てきた部分群のうち、 ![]() であることが言えます。ここで
であることが言えます。ここで![]() は絶対値が1の複素数です。そのことを確認しておきましょう。いま、1次元の複素正方行列とはただの複素数
は絶対値が1の複素数です。そのことを確認しておきましょう。いま、1次元の複素正方行列とはただの複素数![]() のことです。そして、
のことです。そして、
以上に紹介したような行列のつくる群をリー群といいます。ここまで紹介したらリー代数についても触れるべきなのでしょうが、それはまた別の機会にしたいと思います。
今回は、次の議論に入る前の準備として、計算のルールに着目した抽象代数学についてみていきました。その中で、「結合則・単位元・逆元」の3つの基本要素を持つものを群と呼んだのでした。そして「交換則」は一般には成り立たず、交換則が成り立つ特別な場合を加群と呼びました。
後半は、行列の作るリー群について触れました。そこでは2次元での回転を例にして、二つの群が同型になる場合をみました。
さて、次はいよいよ四元数の話に入ります。まずは最初の流れにそって、方程式や因数分解という方向から四元数へ迫ってみたいと思います。その上で、四元数の作る世界についていろいろな角度から掘り下げていくつもりです。